功夫,又称中国功夫和中国传统武术,是中国晚清“武术”的别称,主要体现在个人对武术的运用和造诣上,以“止侵”为技术指导,进入传统的认识人与自然、社会客观规律的教育模式和个人修养。 功夫这个词被两百多年前来到中国的法国传教士称为“传入欧洲的功夫”,但在欧美并没有普及。直到20世纪60年代,随着...
外汇基础知识详解。外汇入门基础知识外汇基础知识是每个投资者都需要了解的重要内容。只有学习了这类交易的基础知识,投资者才有机会成功交易,充分掌握交易的基础知识才是投资者的成功。618外汇网边肖认为,在交易开始时,如果投资者想成功地进行外汇交易,他们需要学习外汇进入的基本知识,这是成功交易的开...
外汇基础知识详解。外汇入门基础知识外汇基础知识是每个投资者都需要了解的重要内容。只有学习了这类交易的基础知识,投资者才有机会成功交易,充分掌握交易的基础知识才是投资者的成功。618外汇网边肖认为,在交易开始时,如果投资者想成功地进行外汇交易,他们需要学习外汇进入的基本知识,这是成功交易的开...
6月30日,海关总署宣布从7月1日起给予基里巴斯共和国进出口关税最惠国待遇,对原产于基里巴斯共和国的进口货物适用最惠国税率。本文通过几个简短的问答,让你对科普下的进口关税税率有一点了解。 1.中国进口关税税率有哪些类型? 《进出口关税条例》第九条规定,进口关税分为最惠国税率、协定税率、优...
6月30日,海关总署宣布从7月1日起给予基里巴斯共和国进出口关税最惠国待遇,对原产于基里巴斯共和国的进口货物适用最惠国税率。本文通过几个简短的问答,让你对科普下的进口关税税率有一点了解。 1.中国进口关税税率有哪些类型? 《进出口关税条例》第九条规定,进口关税分为最惠国税率、协定税率、优...
梦到底是什么?梦的作用是什么?梦发生在睡眠的哪个阶段?做梦会影响人的休息吗?为了梦想,我们有太多的问题。今天,让我们走进心理学的大门,看看那些梦...1.梦是怎么产生的?我们通常用“白日梦”来形容不可能的事情,也就是说,正常情况下,梦是从睡眠中来的,人只有在睡着的时候才能做梦。睡觉时,肌肉处于对健...
梦到底是什么?梦的作用是什么?梦发生在睡眠的哪个阶段?做梦会影响人的休息吗?为了梦想,我们有太多的问题。今天,让我们走进心理学的大门,看看那些梦...1.梦是怎么产生的?我们通常用“白日梦”来形容不可能的事情,也就是说,正常情况下,梦是从睡眠中来的,人只有在睡着的时候才能做梦。睡觉时,肌肉处于对健...
中文写作和百科知识是MTI的必修科目。对于一些刚接触MTI的小伙伴来说,可能不理解为什么英语翻译专业考研会有“中文”科目。有这样的疑惑很正常,因为英语和汉语乍一看是不同的语言系统,所以英语翻译专业的学生不应该考“汉语”。其实这种观点是对翻译的误解。有过一些翻译经验的人会遇到“英语听懂了,汉语表达不...
中文写作和百科知识是MTI的必修科目。对于一些刚接触MTI的小伙伴来说,可能不理解为什么英语翻译专业考研会有“中文”科目。有这样的疑惑很正常,因为英语和汉语乍一看是不同的语言系统,所以英语翻译专业的学生不应该考“汉语”。其实这种观点是对翻译的误解。有过一些翻译经验的人会遇到“英语听懂了,汉语表达不...
冰桶挑战 让我们知道渐冻症 橙色微笑和挑战接力 让我们了解彼得潘病 但是 在这个世界上。 有很多很多我们不知道的罕见疾病 他们就像孤儿 努力在这个世界生存 关于罕见疾病 罕见病,顾名思义,是指罕见病和罕见病,是散布在...
冰桶挑战 让我们知道渐冻症 橙色微笑和挑战接力 让我们了解彼得潘病 但是 在这个世界上。 有很多很多我们不知道的罕见疾病 他们就像孤儿 努力在这个世界生存 关于罕见疾病 罕见病,顾名思义,是指罕见病和罕见病,是散布在...
冰桶挑战 让我们知道渐冻症 橙色微笑和挑战接力 让我们了解彼得潘病 但是 在这个世界上。 有很多很多我们不知道的罕见疾病 他们就像孤儿 努力在这个世界生存 关于罕见疾病 罕见病,顾名思义,是指罕见病和罕见病,是散布在...
冰桶挑战 让我们知道渐冻症 橙色微笑和挑战接力 让我们了解彼得潘病 但是 在这个世界上。 有很多很多我们不知道的罕见疾病 他们就像孤儿 努力在这个世界生存 关于罕见疾病 罕见病,顾名思义,是指罕见病和罕见病,是散布在...

(2)地图的识别
对于给定的一个函数的图像,要从图像的左右、上下范围、变化趋势、对称性等方面研究函数的定义域、范围、单调性、奇偶性,注意图像与分辨率函数中参数的关系。
(3)使用图片
函数图像形象地展示了函数的性质,为研究数量关系问题提供了“形”的直观性。它是探索解决问题的途径和获得问题结果的重要工具。
第二章基本初等函数(ⅰ)
[2.1]指数函数
【2.1.1】指数和指数幂的运算
(1)激进的概念
 {{19}}
{{19}}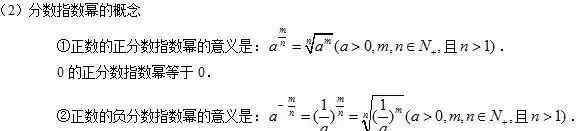 {{21}}${{21}}$
{{21}}${{21}}$【2.1.2】指数函数及其性质
(4)指数函数
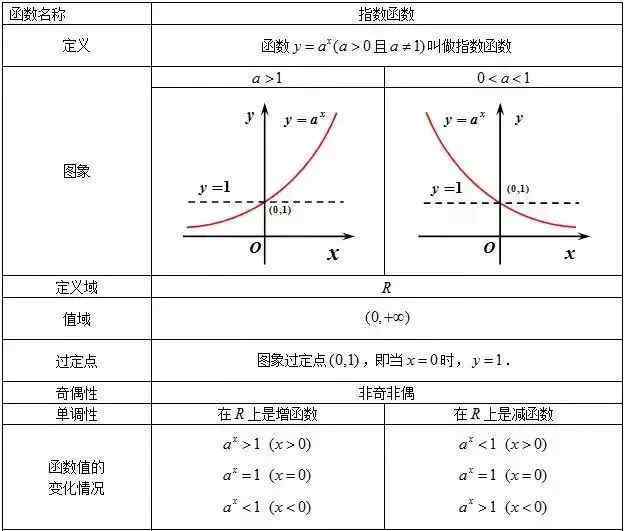
[2.2]对数函数
【2.2.1】对数和对数运算
(1)对数的定义
[2.2.2]对数函数及其性质 {{24}}
{{24}}
(5)对数函数
[2.3]功能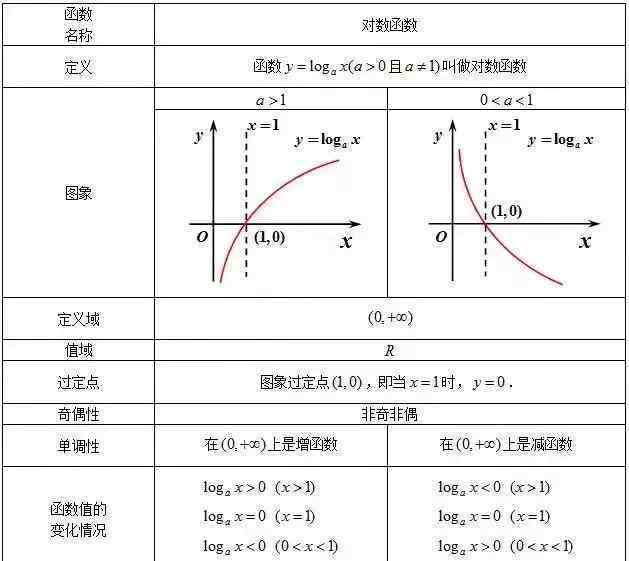 {{27}}
{{27}}
(1)幂函数的定义
一般把函数y=xa叫做幂函数,其中x是自变量,a是常数。
(2)幂函数图像
(3)幂函数的性质
①图像分布:幂函数图像分布在第一、二、三象限,第四象限无图像。幂函数为偶数时,图像分布在第一象限和第二象限(图像为轴对称);当是奇数函数时,图像分布在第一象限和第三象限(图像关于原点对称);当它是非奇数和非偶数函数时,图像仅分布在第一个图像中
②过定点:所有幂函数定义在(0,+∞),图像通过点(1,1)
③单调性:如果a >: 0,则幂函数的图像穿过原点,在[0,+∞)上是增函数。如果a
【补充知识】二次函数 {{30}}${{30}}$
{{30}}${{30}}$(1)二次解析函数的三种形式

(2)求二次分解函数的方法
①已知三点坐标时,应采用通式。
②已知抛物线顶点坐标与对称轴或最大(最小)值有关时,常使用顶点。
③如果已知抛物线与X轴有两个交点,且水平坐标已知,则选择两个公式求f(x)更方便。
(3)二次函数图像的性质
一维二次方程的根的分布是二次函数的重要组成部分。这部分知识虽然涉及到初中代数,但并不系统完整,求解方法侧重于二次方程的根的判别和根与系数关系定理(vieta定理)的应用。基于二次函数图像的性质,系统地分析了一维二次方程实根的分布。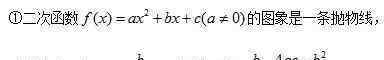 {{33}}
{{33}}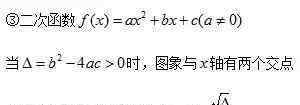
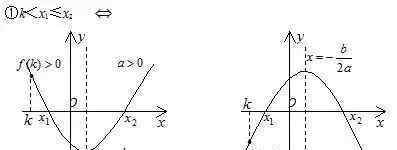 {{36}}
{{36}}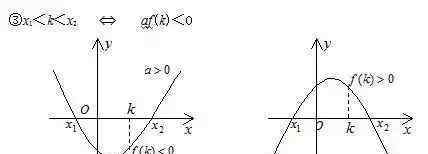 {{38}}
{{38}}
⑥ K1 < X1 < K2 ≤ P1 < X2 < P2可以直接从⑤推导出来。
第三章功能应用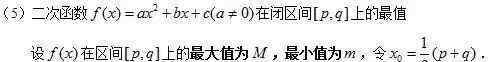 {{41}}
{{41}}
首先,方程的根和函数的零点
本文来源于微信微信官方账号:“爱知教学园”,求学之路,任中任重道远,让我们携手并进,共同努力!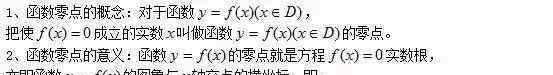 {{44}}${{44}}$
{{44}}${{44}}$

(2)地图的识别
对于给定的一个函数的图像,要从图像的左右、上下范围、变化趋势、对称性等方面研究函数的定义域、范围、单调性、奇偶性,注意图像与分辨率函数中参数的关系。
(3)使用图片
函数图像形象地展示了函数的性质,为研究数量关系问题提供了“形”的直观性。它是探索解决问题的途径和获得问题结果的重要工具。
第二章基本初等函数(ⅰ)
[2.1]指数函数
【2.1.1】指数和指数幂的运算
(1)激进的概念
 {{19}}
{{19}}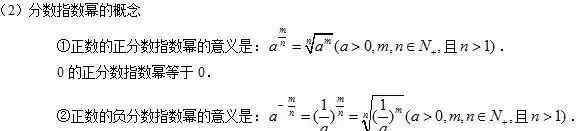 {{21}}${{21}}$
{{21}}${{21}}$【2.1.2】指数函数及其性质
(4)指数函数

[2.2]对数函数
【2.2.1】对数和对数运算
(1)对数的定义
[2.2.2]对数函数及其性质 {{24}}
{{24}}
(5)对数函数
[2.3]功能 {{27}}
{{27}}
(1)幂函数的定义
一般把函数y=xa叫做幂函数,其中x是自变量,a是常数。
(2)幂函数图像
(3)幂函数的性质
①图像分布:幂函数图像分布在第一、二、三象限,第四象限无图像。幂函数为偶数时,图像分布在第一象限和第二象限(图像为轴对称);当是奇数函数时,图像分布在第一象限和第三象限(图像关于原点对称);当它是非奇数和非偶数函数时,图像仅分布在第一个图像中
②过定点:所有幂函数定义在(0,+∞),图像通过点(1,1)
③单调性:如果a >: 0,则幂函数的图像穿过原点,在[0,+∞)上是增函数。如果a
【补充知识】二次函数 {{30}}${{30}}$
{{30}}${{30}}$(1)二次解析函数的三种形式

(2)求二次分解函数的方法
①已知三点坐标时,应采用通式。
②已知抛物线顶点坐标与对称轴或最大(最小)值有关时,常使用顶点。
③如果已知抛物线与X轴有两个交点,且水平坐标已知,则选择两个公式求f(x)更方便。
(3)二次函数图像的性质
一维二次方程的根的分布是二次函数的重要组成部分。这部分知识虽然涉及到初中代数,但并不系统完整,求解方法侧重于二次方程的根的判别和根与系数关系定理(vieta定理)的应用。基于二次函数图像的性质,系统地分析了一维二次方程实根的分布。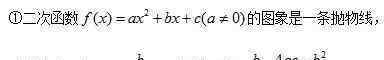 {{33}}
{{33}}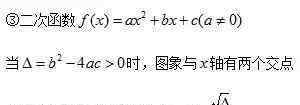
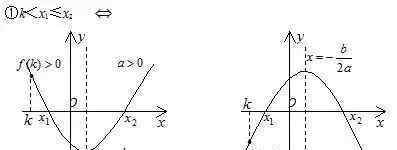 {{36}}
{{36}} {{38}}
{{38}}
⑥ K1 < X1 < K2 ≤ P1 < X2 < P2可以直接从⑤推导出来。
第三章功能应用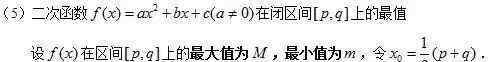 {{41}}
{{41}}
首先,方程的根和函数的零点
本文来源于微信微信官方账号:“爱知教学园”,求学之路,任中任重道远,让我们携手并进,共同努力!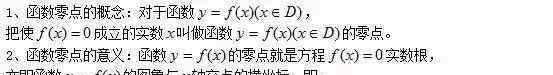 {{44}}${{44}}$
{{44}}${{44}}$

(2)地图的识别
对于给定的一个函数的图像,要从图像的左右、上下范围、变化趋势、对称性等方面研究函数的定义域、范围、单调性、奇偶性,注意图像与分辨率函数中参数的关系。
(3)使用图片
函数图像形象地展示了函数的性质,为研究数量关系问题提供了“形”的直观性。它是探索解决问题的途径和获得问题结果的重要工具。
第二章基本初等函数(ⅰ)
[2.1]指数函数
【2.1.1】指数和指数幂的运算
(1)激进的概念
 {{19}}
{{19}}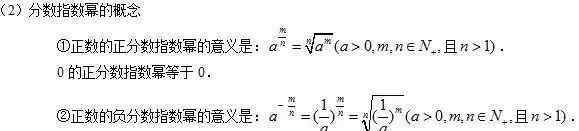 {{21}}${{21}}$
{{21}}${{21}}$【2.1.2】指数函数及其性质
(4)指数函数
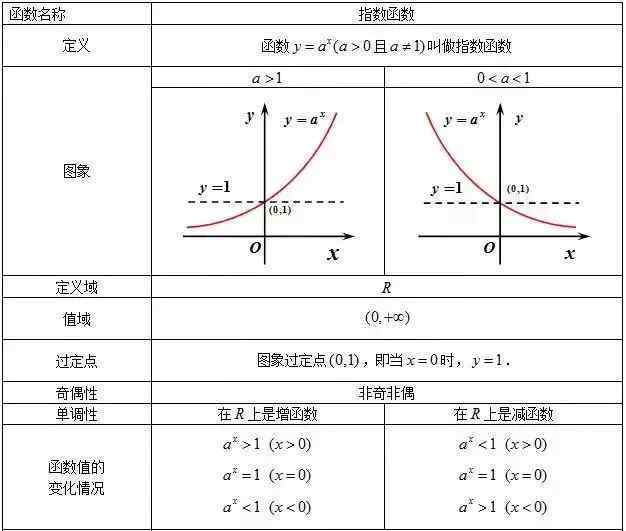
[2.2]对数函数
【2.2.1】对数和对数运算
(1)对数的定义
[2.2.2]对数函数及其性质 {{24}}
{{24}}
(5)对数函数
[2.3]功能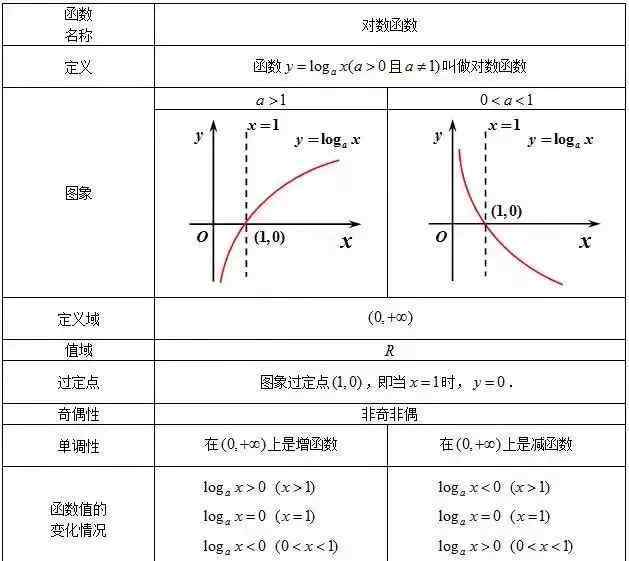 {{27}}
{{27}}
(1)幂函数的定义
一般把函数y=xa叫做幂函数,其中x是自变量,a是常数。
(2)幂函数图像
(3)幂函数的性质
①图像分布:幂函数图像分布在第一、二、三象限,第四象限无图像。幂函数为偶数时,图像分布在第一象限和第二象限(图像为轴对称);当是奇数函数时,图像分布在第一象限和第三象限(图像关于原点对称);当它是非奇数和非偶数函数时,图像仅分布在第一个图像中
②过定点:所有幂函数定义在(0,+∞),图像通过点(1,1)
③单调性:如果a >: 0,则幂函数的图像穿过原点,在[0,+∞)上是增函数。如果a
【补充知识】二次函数 {{30}}${{30}}$
{{30}}${{30}}$(1)二次解析函数的三种形式
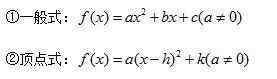
(2)求二次分解函数的方法
①已知三点坐标时,应采用通式。
②已知抛物线顶点坐标与对称轴或最大(最小)值有关时,常使用顶点。
③如果已知抛物线与X轴有两个交点,且水平坐标已知,则选择两个公式求f(x)更方便。
(3)二次函数图像的性质
一维二次方程的根的分布是二次函数的重要组成部分。这部分知识虽然涉及到初中代数,但并不系统完整,求解方法侧重于二次方程的根的判别和根与系数关系定理(vieta定理)的应用。基于二次函数图像的性质,系统地分析了一维二次方程实根的分布。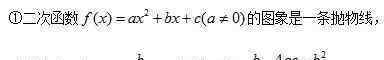 {{33}}
{{33}}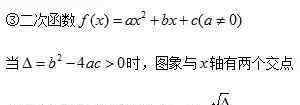
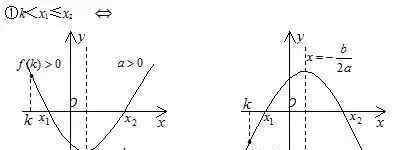 {{36}}
{{36}}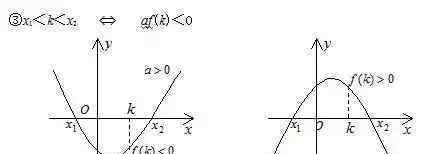 {{38}}
{{38}}
⑥ K1 < X1 < K2 ≤ P1 < X2 < P2可以直接从⑤推导出来。
第三章功能应用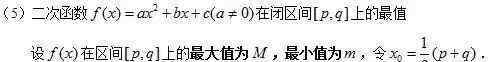 {{41}}
{{41}}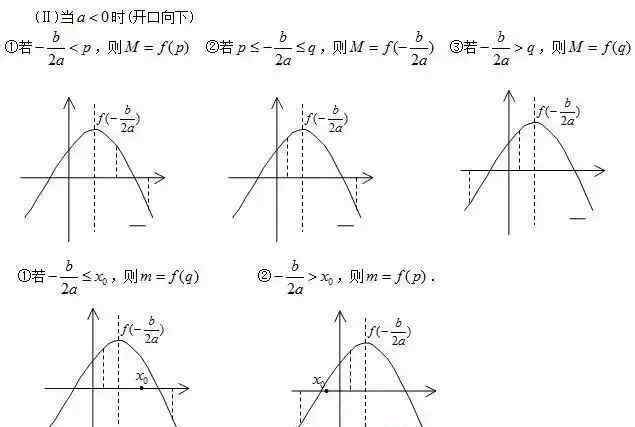
首先,方程的根和函数的零点
本文来源于微信微信官方账号:“爱知教学园”,求学之路,任中任重道远,让我们携手并进,共同努力!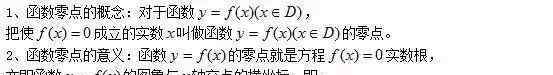 {{44}}${{44}}$
{{44}}${{44}}$

(2)地图的识别
对于给定的一个函数的图像,要从图像的左右、上下范围、变化趋势、对称性等方面研究函数的定义域、范围、单调性、奇偶性,注意图像与分辨率函数中参数的关系。
(3)使用图片
函数图像形象地展示了函数的性质,为研究数量关系问题提供了“形”的直观性。它是探索解决问题的途径和获得问题结果的重要工具。
第二章基本初等函数(ⅰ)
[2.1]指数函数
【2.1.1】指数和指数幂的运算
(1)激进的概念
 {{19}}
{{19}}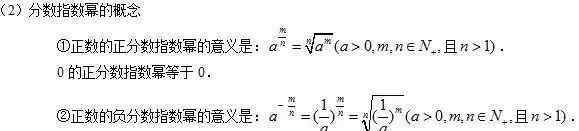 {{21}}${{21}}$
{{21}}${{21}}$【2.1.2】指数函数及其性质
(4)指数函数

[2.2]对数函数
【2.2.1】对数和对数运算
(1)对数的定义
[2.2.2]对数函数及其性质 {{24}}
{{24}}
(5)对数函数
[2.3]功能 {{27}}
{{27}}
(1)幂函数的定义
一般把函数y=xa叫做幂函数,其中x是自变量,a是常数。
(2)幂函数图像
(3)幂函数的性质
①图像分布:幂函数图像分布在第一、二、三象限,第四象限无图像。幂函数为偶数时,图像分布在第一象限和第二象限(图像为轴对称);当是奇数函数时,图像分布在第一象限和第三象限(图像关于原点对称);当它是非奇数和非偶数函数时,图像仅分布在第一个图像中
②过定点:所有幂函数定义在(0,+∞),图像通过点(1,1)
③单调性:如果a >: 0,则幂函数的图像穿过原点,在[0,+∞)上是增函数。如果a
【补充知识】二次函数 {{30}}${{30}}$
{{30}}${{30}}$(1)二次解析函数的三种形式
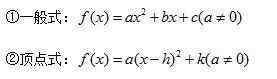
(2)求二次分解函数的方法
①已知三点坐标时,应采用通式。
②已知抛物线顶点坐标与对称轴或最大(最小)值有关时,常使用顶点。
③如果已知抛物线与X轴有两个交点,且水平坐标已知,则选择两个公式求f(x)更方便。
(3)二次函数图像的性质
一维二次方程的根的分布是二次函数的重要组成部分。这部分知识虽然涉及到初中代数,但并不系统完整,求解方法侧重于二次方程的根的判别和根与系数关系定理(vieta定理)的应用。基于二次函数图像的性质,系统地分析了一维二次方程实根的分布。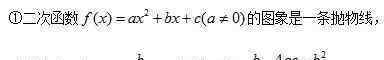 {{33}}
{{33}}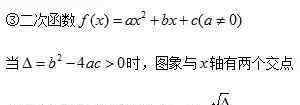
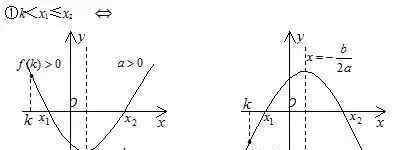 {{36}}
{{36}} {{38}}
{{38}}
⑥ K1 < X1 < K2 ≤ P1 < X2 < P2可以直接从⑤推导出来。
第三章功能应用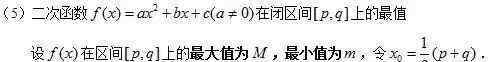 {{41}}
{{41}}
首先,方程的根和函数的零点
本文来源于微信微信官方账号:“爱知教学园”,求学之路,任中任重道远,让我们携手并进,共同努力!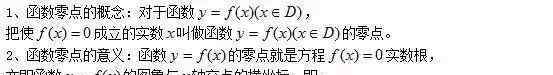 {{44}}${{44}}$
{{44}}${{44}}$










 {{19}}
{{19}}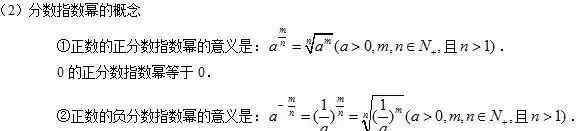 {{21}}${{21}}$
{{21}}${{21}}$
 {{24}}
{{24}}
 {{27}}
{{27}}
 {{30}}${{30}}$
{{30}}${{30}}$
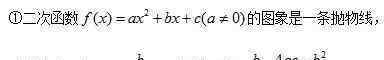 {{33}}
{{33}}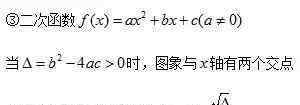
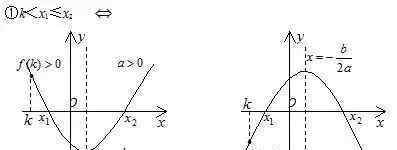 {{36}}
{{36}} {{38}}
{{38}}
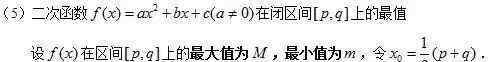 {{41}}
{{41}}
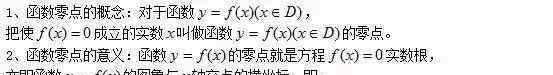 {{44}}${{44}}$
{{44}}${{44}}$

 {{19}}
{{19}}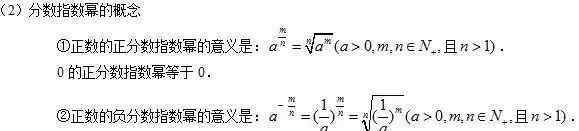 {{21}}${{21}}$
{{21}}${{21}}$
 {{24}}
{{24}}
 {{27}}
{{27}}
 {{30}}${{30}}$
{{30}}${{30}}$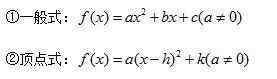
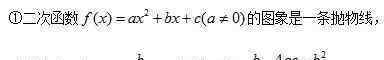 {{33}}
{{33}}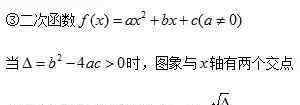
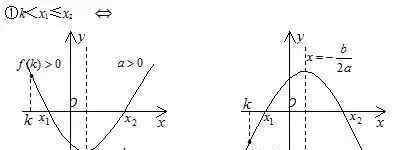 {{36}}
{{36}} {{38}}
{{38}}
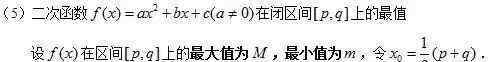 {{41}}
{{41}}
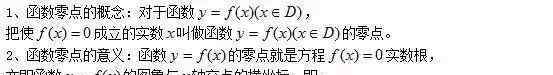 {{44}}${{44}}$
{{44}}${{44}}$